Measure, Probability, and Mathematical Finance: A Problem-Oriented Approach

CHAPTER 17

CHARACTERISTIC FUNCTIONS

Characteristic functions provide an important tool to study the distributional properties of random variables and sums of independent random variables. In particular, characteristic functions can be used to characterize the probability distribution of a random variable and to identify the limit distribution of a sequence of random variables. In this chapter, we present characteristic functions and relevant results.

17.1 Basic Concepts and Facts

Definition 17.1 (Moment Generating Function). Let X be a random variable. Then the moment generating function of X is defined as

(17.1)

The moment generating function of a random vector X = (X₁, X₂,…., X_n)^T is defined as

(17.2)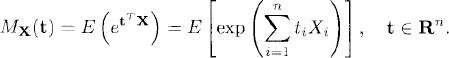

Definition 17.2 (Cumulant Generating Function). Let X be a random variable. Then the cumulant generating function of X is defined as

(17.3)

where M_X (h) is the moment generating function of X.

Definition 17.3 (Characteristic Function of Random Variables). Let X be a random variable. Then the characteristic function of X is defined as

(17.4)

where is the imaginary number.

The characteristic ...