CHAPTER 7
THE RADON-NIKODYM THEOREM
The Radon-Nikodym theorem is a fundamental and important result in measure theory and has important applications in modern probability theory. For example, the Radon-Nikodym theorem can be used to prove the existence of conditional expectations (Klenke, 2006). In this chapter, we present some concepts and results related to this theorem.
7.1 Basic Concepts and Facts
Definition 7.1 (Signed Measure). A signed measure on a σ-algebra is a set function μ : ∑ → 
that is countably additive:
) = 0.
n 
∑, n = 1, 2,…, have
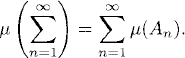
Definition 7.2 (Absolute Continuity). Let (S, ∑, μ) be a measure space and λ a signed measure on ∑. The signed measure λ is said to be absolutely continuous with respect to μ, denoted by λ 
μ, if and only if μ(A) = 0 (A ∑) implies λ(A) = 0.
Definition 7.3 (Equivalent Measures). Let μ and λ be two measures defined ...
Get Measure, Probability, and Mathematical Finance: A Problem-Oriented Approach now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.
