CHAPTER 20
CENTRAL LIMIT THEOREMS
The central limit theorem is a very important result in probability theory. It states that the mean of a sufficiently large number of independent random variables will be approximately normally distributed under certain conditions. The central limit theorem has several versions. In this chapter, we present some central limit theorems.
20.1 Basic Concepts and Facts
Definition 20.1 (Degenerate Distribution). A distribution function is said to be degenerate if it is equal to Δx0 for some x0, where Δx0 is defined as
(20.1)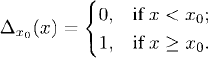 
Definition 20.2 (Weak Convergence). A sequence {Fn}n≥1 of distribution functions is said to converge weakly to a distribution function F, written as Fn 
F or Fn(x) 
F(x), if
where 
(F) = {x 
R : F is continuous at x}.
Definition 20.3 (Convergence in Distribution). Let {Xn}n≥1 be a sequence of random variables. The sequence is said to converge ...
Get Measure, Probability, and Mathematical Finance: A Problem-Oriented Approach now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.
