CHAPTER 6
LEBESGUE INTEGRATION
Lebesgue integration is the general theory of integration of a function with respect to a general measure. In this chapter, we present some concepts and theorems used to develop the Lebesgue integration theory.
6.1 Basic Concepts and Facts
Definition 6.1 (Simple Function). Let (S, ∑) be a measurable space and (m∑)+ denote the set of all nonnegative ∑-measurable functions. An element f of (m∑)+ is considered simple if f can be written as a finite sum
(6.1) 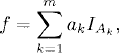
where ak ![]() [0, ∞] and
[0, ∞] and ![]() k
k ![]() ∑ for k = 1, 2,…, m. The set of all nonnegative simple functions is denoted by SF+.
∑ for k = 1, 2,…, m. The set of all nonnegative simple functions is denoted by SF+.
Definition 6.2 (Integral of Nonnegative Simple Functions). Let (S, ∑, μ) be a measure space, and let
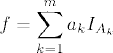
be a nonnegative simple function on S. The integral of f with respect to μ is defined as
Definition 6.3 (Integral of Nonnegative Measurable Functions). Let (S, ∑, μ) be a measure space and (m
Get Measure, Probability, and Mathematical Finance: A Problem-Oriented Approach now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.