CHAPTER 43
PATH-DEPENDENT OPTIONS
Path-dependent options are also referred to as “exotic options”, whose payoffs depend on the path of the underlying asset. In this chapter, we present pricing formulas for some path-dependent options within the Black-Scholes framework.
43.1 Basic Concepts and Facts
Theorem 43.1 (European Barrier Option Price). Let {(X(0)t, Xt) : 0 ≤ t ≤ T} be the Black-Scholes market given in Definition 42.2. Let
(43.1b) ![]()
(43.1c) 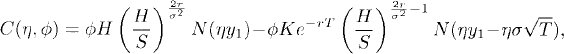
and
(43.1d) 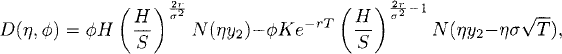
where S = X0 is the initial price of the risky asset, K is the strike, T is the expiration time, H is the barrier, N(·) is as defined in Equation (42.1c), and
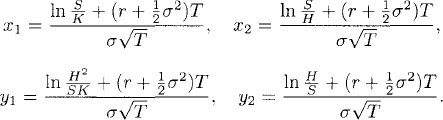
Then
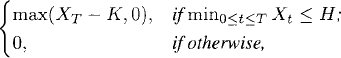
(43.2) 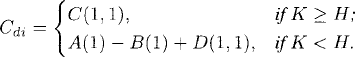
Get Measure, Probability, and Mathematical Finance: A Problem-Oriented Approach now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

