RF and Microwave Engineering: Fundamentals of Wireless Communications

5.3 Scattering Parameters and Power

The power waves a_i and b_i of a two-port network are related by the following system of linear equations as

5.13

5.14

where the coefficients s_ij are the scattering parameters [4]. We can write the equations in matrix form as

5.15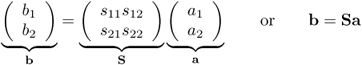

where S is the scattering matrix. Matrix elements s_ii with equal indices are reflection coefficients describing reflection of waves at port i. Matrix elements s_ij with different indices i ≠ j are transmission coefficients, describing the transmission of waves from port j to port i.

From Section 3.1 we already know reflection coefficients r. In order to understand that the scattering parameters with two identical indices s_ii are reflection coefficients too, we look at Equation 5.13, which is given by b₁ = s₁₁a₁ + s₁₂a₂. Let us assume that port 2 is terminated by an infinite transmission line with a characteristic impedance of Z₀₂. On this transmission line no incident wave a₂ exists. Hence, a₂ = 0. (Alternatively, we can terminate port 2 with a resistor that equals the characteristic line impedance of that port R = Z₀₂.) Due to Ohm's law the resistor enforces U₂ = Z₀₂(−I₂). The minus sign stems from our definition of voltage ...