Graph Example: Topological Sorting
Sometimes we encounter problems in which we must determine an acceptable ordering by which to carry out tasks that depend on one another. Imagine a set of classes at a university that have prerequisites, or a complicated project in which certain phases must be completed before other phases can begin. To model problems like these, we use a directed graph, called a precedence graph , in which vertices represent tasks and edges represent dependencies between them. To show a dependency, we draw an edge from the task that must be completed first to the task that depends on it.
For example, consider the directed acyclic graph in Figure 11.9a, which represents a curriculum of seven courses and their prerequisites: CS100 has no prerequisites, CS200 requires CS100, CS300 requires CS200 and MA100, MA100 has no prerequisites, MA200 requires MA100, MA300 requires CS300 and MA200, and CS150 has no prerequisites and is not a prerequisite itself.
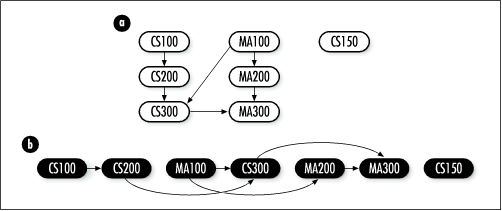
Depth-first search helps to determine an acceptable ordering by performing a topological sort on the courses. Topological sorting orders the vertices in a directed acyclic graph so that all edges go from left to right. In the problem involving course prerequisites, this means that all prerequisites will appear ...
Get Mastering Algorithms with C now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

