This is the less intuitive assumption, but it can be extremely useful to reduce the complexity of many problems. First of all, we can provide a non-rigorous definition of a manifold. An n-manifold is a topological space that is globally curved, but locally homeomorphic to an n-dimensional Euclidean space. In the following diagram, there's an example of a manifold: the surface of a sphere in ℜ3:
2D manifold obtained from a spherical surface
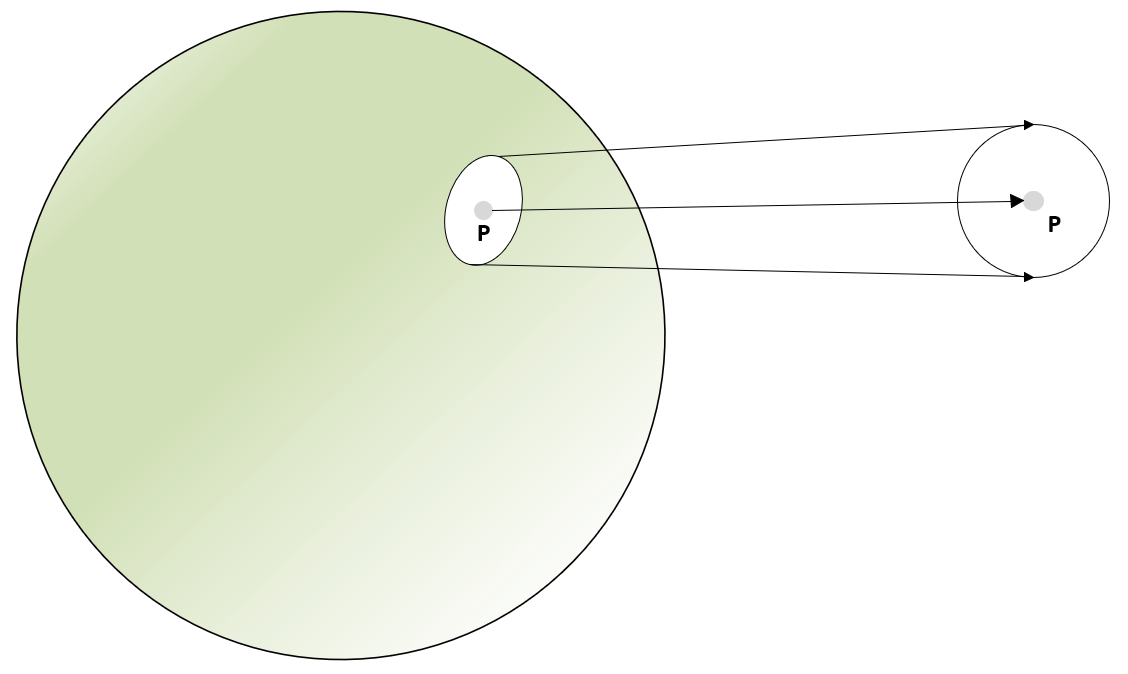
The small patch around P (for ε → 0) can be mapped to a flat circular surface. Therefore, the properties of a manifold are locally based on the Euclidean geometry, while, globally, they ...
