8.1. Trigonometric Functions of Any Angle
In Chap. 7 we defined the sine, cosine, and tangent of acute angles. We did this in terms of the sides of a right triangle, and also for an angle in standard position. Let us now expand this definition to angles of any size.
We also introduce three new trigonometric functions, the cotangent, secant, and cosecant. Their definitions, along with the sine, cosine, and tangent, are

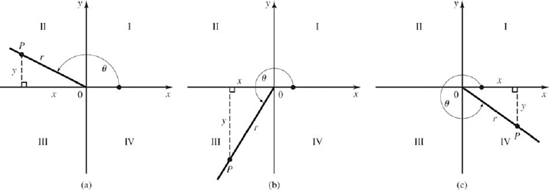
Figure 8-3 shows angles in the second, third, and fourth quadrants. The trigonometric functions of any of these angles are defined exactly as for an acute angle in quadrant I. From any point P on the terminal side of the angle we drop a perpendicular to the x axis, forming a right triangle with legs x and y and with a hypotenuse r. The six trigonometric functions are then given by Eqs. 111 through 113, just as before, except that some of the functions are now negative.
Figure 8.3. FIGURE 8-3
Example 1:A point on the terminal side of angle θ has the coordinates (−3, −5). Write the six trigonometric functions of θ to three significant digits. Solution: We sketch the angle as shown in Fig. 8-4 and see that it lies in the third quadrant. We find distance r by the Pythagorean theorem. Then, |
Figure 8.4. FIGURE 8-4
8.1.1. Trigonometric Functions of Any Angle by ...
Get Technical Mathematics, Sixth Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

