Synthesis of Arithmetic Circuits: FPGA, ASIC and Embedded Systems

14.2 POLYNOMIAL COMPUTATION CIRCUITS

Polynomial approximation methods are often used to calculate special functions such as logarithmic, exponential, of trigonometric (Chapter 7). In Section 7.3.2 a recursive multilevel computation scheme was proposed as a generalization of the Hörner expansion technique to compute polynomials: the generalized Horner expansion (GHE). Using formulas (7.30)–(7.32), the example suggested in Section 7.3.2 is implemented in this section. The example consists of a 3-level GHE implementing a degree-63 polynomial to be computed in 9 multiply-and-add steps. First, 16 degree-3 polynomials can be computed (3 steps); then four degree-15 polynomials are worked out using the degree-3 polynomials as primitives (3 steps); another 3 steps are finally needed to compute the degree-63 polynomial using the degree-16 ones as primitives. The respective cells to be implemented correspond to the following polynomials:

First stage cells (Figure 14.14a)

Second stage cells (Figure 14.15a)

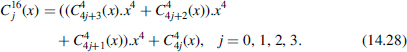
Figure 14.14 GHE degree-63 polynomial: first stage.

Figure 14.15 GHE degree-63 polynomial: ...