Introduction to Digital Systems: Modeling, Synthesis, and Simulation Using VHDL

2.5 SIGNED AND UNSIGNED NUMBERS

Unsigned binary numbers are, by definition, positive numbers and thus do not require an arithmetic sign. An m-bit unsigned number represents all numbers in the range 0 to 2^m − 1. For example, the range of 8-bit unsigned binary numbers is from 0 to 255₁₀ in decimal and from 00 to FF₁₆ in hexadecimal. Similarly, the range of 16-bit unsigned binary numbers is from 0 to 65,535₁₀ in decimal and from 0000 to FFFF₁₆ in hexadecimal.

Signed numbers, on the other hand, require an arithmetic sign. The most significant bit of a binary number is used to represent the sign bit. If the sign bit is equal to zero, the signed binary number is positive; otherwise, it is negative. The remaining bits represent the actual number. There are three ways to represent negative numbers.

2.5.1 Sign-Magnitude Representation

In the sign-magnitude representation method, a number is represented in its binary form. The most significant bit (MSB) represents the sign. A 1 in the MSB bit position denotes a negative number; a 0 denotes a positive number. The remaining n −1 bits are preserved and represent the magnitude of the number. The following examples illustrate the sign-magnitude representation:

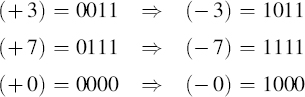
2.5.2 One's-Complement Representation

In the one's-complement form, the MSB represents the sign. The remaining bits are inverted for negative numbers only. Positive numbers are represented ...