Process Control: Modeling, Design, and Simulation

3.2. Linear State Space Models

In Chapter 2 we developed fundamental models, which were normally nonlinear in nature. We then developed state space models that were based on linearizing the fundamental models at a steady-state solution. This led to the notion of a perturbation or deviation variable, which is simply the perturbation of a variable from its steady-state value.

State space models have the following form, where the states (x), inputs (u), and outputs (y) are all perturbation or deviation variables

Equation 3.1

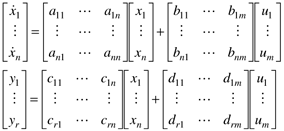
Recall that in matrix notation, the first subscript refers to the row and the second subscript refers to the column. When matrices ...