Hands-On Machine Learning for Algorithmic Trading

The curse of dimensionality

An increase in the number of dimensions of a dataset means there are more entries in the vector of features that represents each observation in the corresponding Euclidean space. We measure the distance in a vector space using Euclidean distance, also known as the L2 norm, which we applied to the vector of linear regression coefficients to train a regularized Ridge Regression model.

The Euclidean distance between two n-dimensional vectors with Cartesian coordinates p = (p₁, p₂, ..., p_n) and q = (q₁, q₂, ..., q_n) is computed using the familiar formula developed by Pythagoras:

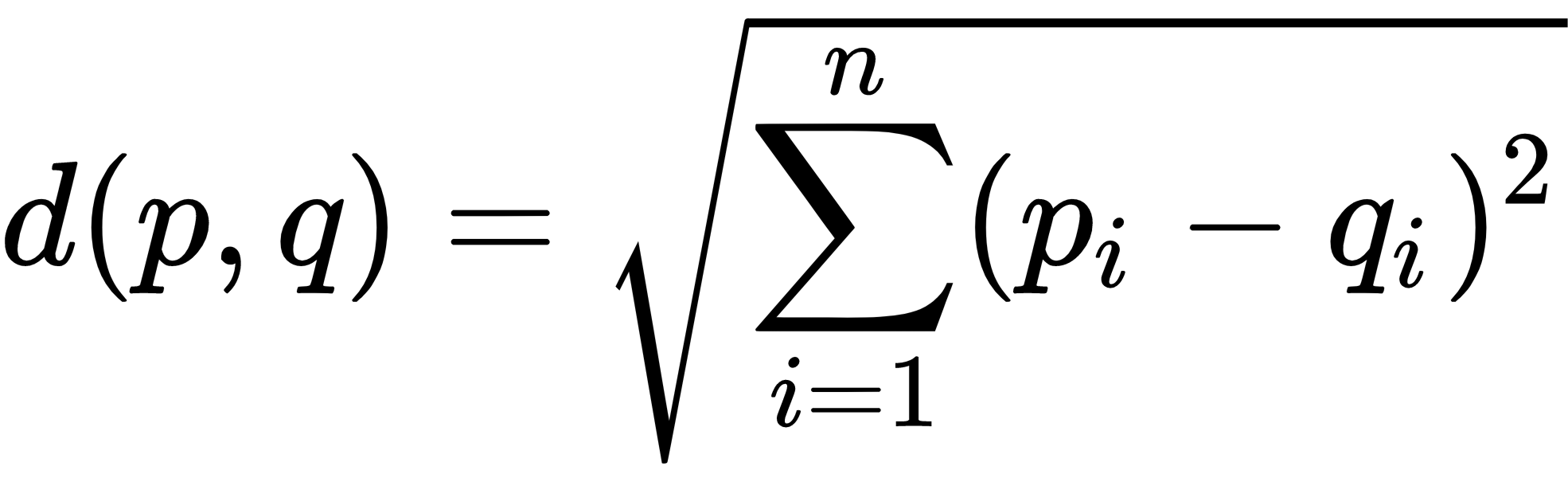
Hence, each new dimension adds a non-negative ...