Hands-On Machine Learning for Algorithmic Trading

PCA based on the covariance matrix

We first compute the principal components using the square covariance matrix with the pairwise sample covariances for the features x_i, x_j, i, j = 1, ..., n as entries in row i and column j:

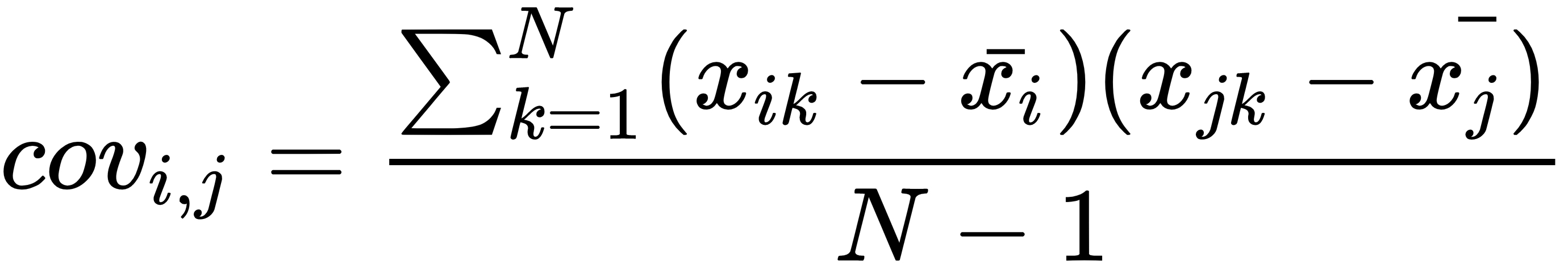
For a square matrix M of n dimensions, we define the eigenvectors ω_i and eigenvalues λ_i, i=1, ..., n as follows:

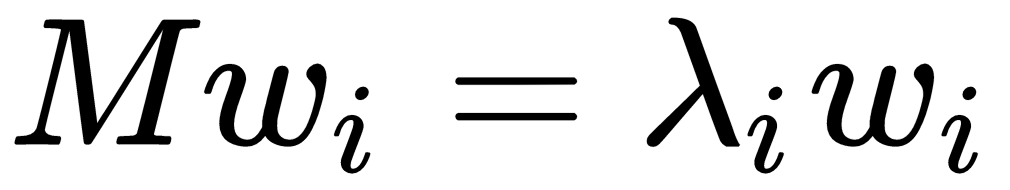
Hence, we can represent the matrix M using eigenvectors and eigenvalues, where W is a matrix that contains the eigenvectors as column vectors, and L is a matrix that contains the λ_i as diagonal entries (and 0s ...