Pythonデータサイエンスハンドブック ―Jupyter、NumPy、pandas、Matplotlib、scikit-learnを使ったデータ分析、機械学習

456

5

章 機械学習

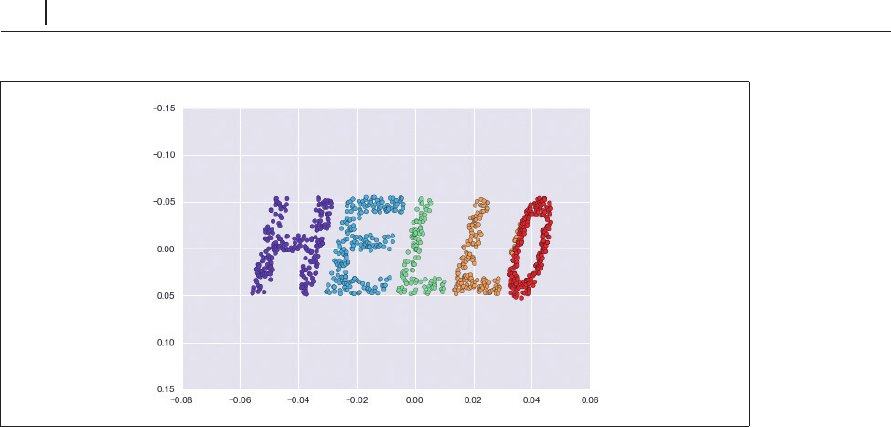
図5-103　局所線形埋め込みによる非線形に埋め込まれた入力からの元データ復元

結果は元の多様体に比べて多少歪みがありますが、データの本質的な関係を捉えています。

5.10.6

 多様体学習に対する考察

ここまでの事例には説得力がありましたが、実際のところ多様体学習の手法は多少難解な点もあ

るため、高次元データの単純で定性的な可視化以外で使用することはあまりありません。

以下は、多様体学習に関するさまざまな課題であり、

PCA

と比較して劣っていると考えられる

点です。

●

多様体学習には、欠損データを処理するための良いフレームワークがありません。対照的に、

PCA

には欠落データに対する直接的かつ反復なアプローチがあります。

●

多様体学習では、データにノイズが存在すると多様体を「短絡」させ、埋め込みを大幅に変化

させます。対照的に、

PCA

は、最も重要な成分からノイズを自然に除去します。

●

多様体学習の一般的な埋め

込み結果は選択された近傍の数に大きく依存しますが、最適な数

の近傍を選択するための一般的な定量的方法は存在しません。対照的に、

PCA

はそのような

選択が必要ありません。

●

多様体学習では、最適な出力次元の数を決定することは困難です。対照的に、

PCA

では因子

寄与率に基づいて最適な出力次元を見つけることができます。

●

多様体学習において、埋め込まれた次元の意味は必ずしも明確ではありません。一方

PCA

で

は、主成分は非常に明確な意味を持ちます。

●

多様体学習の計算コストは

O

[

N

2